Answer:
r = 3519.55 m
Step-by-step explanation:
We know that the acceleration of a particle in a circular motion is directed towards the center of the circumference and has magnitude:
F = rω^2
Where r is the radius of the circumference and ω is the angular velocity.
From the two acceleration vectors we find that their magnitude is
√(7^2+6^2) = √85
Therefore:
√85 m/s^2= rω^2
Now we need to calculate the angular velocity to obtain the radius. Since t2-t1 = 3s is less than one period we can be sure that the angular velocity is equals to the angle traveled between this time divided by 3 s.
The angle with respect to the x-axis for the particle at t1 and t2 is:
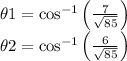
Therefore, the angular velocity ω is (in radians per second):
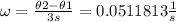
Therefore:
r = √85 / (0.0511813)^2 = 3519.55 m