Question

Suppose that salaries for recent graduates of one university have a mean of $25,500 with a standard deviation of $1050. Using Chebyshev's Theorem, what is the minimum percentage of recent graduates who have salaries between $22,350 and $28,650? Round your answer to one decimal place.

Answer 1

88.9%

Explanation:

Given:

Mean salary for the graduates = $25,500

Standard deviation = $1050

Minimum salary = $22,350

Maximum salary = $28,650

Now,

Using Chebyshev's Theorem

Percentage =
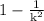`1-\frac{\textup{1}}{\textup{k}^2}` ................(1)

here,

The value of 'k' is calculated as:

k =
`\frac{\textup{Maximum value - Mean}}{\textup{standard deviation}}`

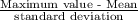
on substituting the values, we get

k =
`(\$28,650 - \$25,500)/(\$1050)`

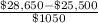
or

k = 3

on substituting the value of k in (1), we get

Percentage =
`1-\frac{\textup{1}}{\textup{3}^2}`

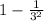
or

Percentage =
`1-\frac{\textup{1}}{\textup{9}}`

or

Percentage = 88.9%