Answer:
the probability that exactly 30 of the 500 calculators IS 0.0495
Step-by-step explanation:
Given data:
number of calculators n = 500,
percentage of defected calculators p = 0.05
From Normal approximation method;
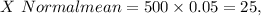
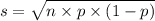
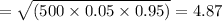
Therefore probability is
P(X= 30) = P(29.5< X< 30.5) ( from continuous correction)
![=P[((29.5-25))/(4.87)] < ((X-mean))/(s) < ((30.5-25))/(4.87) </p><p> =P(0.92<Z< 1.13)](https://img.qammunity.org/2020/formulas/business/college/akc0b4p4cqxls13frpqk34ngqsb29cbb8k.png)
=0.0495 (from standard table of Z )