Answer:
Ans.
a) The value of the invesment of an annuity of $4,350, at 6% for 15 years is $42.248,28
b) If it was for 40 years, the value of the investment would be: $65.451,39
c) If it was for 75 years, the value of the investment would be: $71.582,94
d) If it was forever, the value of the investment would be: $72.500
Step-by-step explanation:
Hi, all we have to do is solve for "PV" the following equation for all the conditions of the problem, here is the equation.
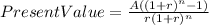
Where:
A= Annuity or yearly payment ($4,350)
r = require rate of return, in our case 0.06
n= periods to pay
This equation can be used with all the questions of the problem but d) which requires that we use the following equation.
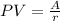
Now, let´s see how to solve all this step by step.
a)

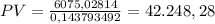
b)
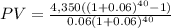
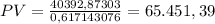
c)
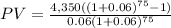

d)
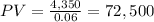
Best of luck