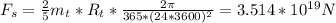Answer:

Step-by-step explanation:
We know that torque exerted by superman is given by:
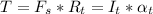 where It is earth's inertia, and αt is earth acceleration.
where It is earth's inertia, and αt is earth acceleration.
The inertia of a solid sphere is calculated as:
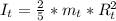
Earth's acceleration is:

Where t is the lapse of 1 year. t = 365*24*3600 = 31536000s
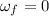
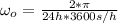
Solving for the acceleration and replacing the values:
 Replacing this value on the torque equation:
Replacing this value on the torque equation: