Answer:
a) Speed of the particle at this instant
v = 8.43 m/s
b) Speed of the particle at (1/8) revolution later
v = 14.83 m/s
Step-by-step explanation:
We apply the equations of circular motion uniformly accelerated :
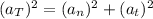 Formula (1)
Formula (1)
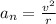 Formula (2)
Formula (2)
 Formula (3)
Formula (3)
v= ω*r Formula (4)
ω² = ω₀² + 2*α*θ Formula (5)
Where:
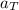 : total acceleration, (m/s²)
: total acceleration, (m/s²)
 : normal acceleration, (m/s²)
: normal acceleration, (m/s²)
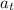 : tangential acceleration, (m/s²)
: tangential acceleration, (m/s²)
 : angular acceleration (rad/s²)
: angular acceleration (rad/s²)
r : radius of the circular path (m)
v : tangential velocity (m/s)
ω : angular speed ( rad/s)
ω₀: initial angular speed ( rad/s)
θ : angle that the particle travels (rad)
Data:
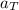 = 15 m/s²
= 15 m/s²
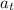 = 12 m/s²
= 12 m/s²
r=7.90 m :radius of the circular path
Problem development
In the formula (1) :
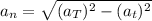
We replace the data
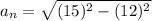
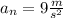
We use formula (2) to calculate v:
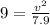 Equation (1)
Equation (1)
a)Speed of the particle at this instant
in the equation (1):
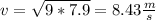
b)Speed of the particle at (1/8) revolution later
We know the following data:
θ =(1/8) revolution=( 1/8) *2π= π/4
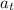 = 12 m/s²
= 12 m/s²
v₀= 8.43 m/s
r=7.9 m
We use formula (3) to calculate α


We use formula (4) to calculate ω₀
v₀= ω₀ *r
8.43 = ω₀*7.9
ω₀ = 8.43/7.9 = 1.067 rad/s
We use formula (5) to calculate ω
ω² = ω₀² + 2*α*θ
ω²= (1.067)² + 2*1.52*π/4
ω² =3.526
ω = 1.87 rad/s
We use formula (4) to calculate v
v= 1.87 rad/s * 7.9m
v = 14.83 m/s : speed of the particle at (1/8) revolution later