Question

Considering the same population of cats as in Part A, what is the expected frequency of each genotype (TLTL, TLTS, TSTS ) based on the equation for Hardy-Weinberg equilibrium? Keep in mind that you just learned in Part A that: The allele frequency of TL is 0.4. The allele frequency of TS is 0.6. The equation for Hardy-Weinberg equilibrium states that at a locus with two alleles, as in this cat population, the three genotypes will occur in specific proportions: p2+2pq+q2=1 Enter the values for the expected frequency of each genotype: TLTL, TLTS, and TSTS. Enter your answers numerically to two decimal places, not as percentages. For help applying the Hardy-Weinberg equation to this cat population, see Hints 1 and 2.

Answer 1

P = f(TLTL) = 0,16

H = f(TLTS) = 0,48

Q = f(TSTS) = 0,36

Step-by-step explanation:

Hello!

The allele proportion of any locus defines the genetic constitution of a population. Its sum is 1 and its values ​​can vary between 0 (absent allele) and 1 (fixed allele).

The calculation of allelic frequencies of a population is made taking into account that homozygotes have two identical alleles and heterozygotes have two different alleles.

In this case, let's say:

f(TL) = p

f(TS) = q

p + q = 1

Considering the genotypes TLTL, TLTS, TSTS, and the allele frequencies:

TL= 0,4

TS= 0,6

Genotypic frequency is the relative proportion of genotypes in a population for the locus in question, that is, the number of times the genotype appears in a population.

P = f(TLTL)

H = f(TLTS)

Q = f(TSTS)

Also P + H + Q = 1

And using the equation for Hardy-Weinberg equilibrium, the genotypic frequencies of equilibrium are given by the development of the binomial:

`p^(2) = f(TLTL)`

`2pq = f(TSTL)`

`q^(2) = f(TSTS)`

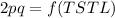
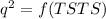
So, if the population is in balance:

`P = p^(2)`

`H = 2pq`

`Q = q^(2)`

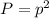
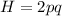
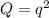
Replacing the given values of allele frecuencies in each equiation you can calculate the expected frequency of each genotype for the next generation as:

`f(TLTL) = P = p^(2) = 0,4^(2) = 0,16`

`f(TLTS) = H = 2pq = 2*0,4*0,6 = 0,48`

`f(TSTS) = Q = q^(2) = 0,6^(2) = 0,36`

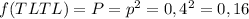
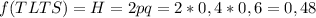
I hope you have a SUPER day!