Question

F(x)= 1/2 x + 3 a linear, quadratic, exponential function or none of those

Answer 1

linear

The problem:

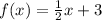`f(x)=(1)/(2)x+3` is linear, quadratic, exponential, or none of these?

Explanation:

If the function is
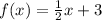`f(x)=(1)/(2)x+3` then f is linear.

It is linear because it is a polynomial with first degree.

It is linear because you can compare it to the slope-intercept form of a linear equation which is y=mx+b. We see thatm=1/2 and b=3.

Example of quadratics:

`a(x)=4x^2+3x+1`

`b(x)=5x^2+1`

`c(x)=5x^2-x`

`d(x)=5x^2`

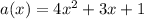
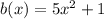
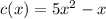
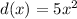
All the functions a through d are quadratics because they are polynomials with degree 2.

Also each one of them are comparable to the quadratic expression:

`ax^2+bx+c`.

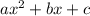Examples of exponential:

`e(x)=5^x`

`g(x)=5 \cdot 3^(3x)`

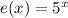
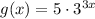
Notice all of these have a variable exponent on a constant base.