Question

A lead ball is dropped in a lake from a diving board 5.20 m above the water. It hits the water with a certain velocity and then sinks to the bottom with this same constant velocity. It reaches the bottom 4.80 s after it is dropped. (a) How deep is the lake? What are the (b) magnitude and (c) direction (up or down) of the average velocity of the ball for the entire fall? Suppose that all the water is drained from the lake. The ball is now thrown from the diving board so that it again reaches the bottom in 4.80 s. What are the (d) magnitude and (e) direction of the initial velocity of the ball?

Answer 1

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration due to gravity = 9.81 m/s²

Here, downward direction is considered positive

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* 9.81* 5.2+0^2)\\\Rightarrow v=10.1\ m/s`

`v=u+at\\\Rightarrow 10.1=0+9.81t\\\Rightarrow t=(10.1)/(9.81)=1.03\ s`

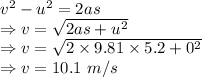
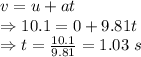
Time taken by the ball to reach the water is 1.03 seconds

Time in the water = 4.8 - 1.03 = 3.77 seconds

Distance = Speed × Time

⇒Distance = 10.1×3.77 = 38.077 m.

The lake is 38.077 m deep

Total distance the ball traveled is 5.2+38.077 = 43.277 m

Average velocity

`v_(avg)=(43.277)/(4.8)=9.02\ m/s`

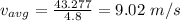
Average velocity = 9.02 m/s Downward

Now, s = 43.277 m

t = 4.8 seconds

`s=ut+(1)/(2)at^2\\\Rightarrow u=(s-(1)/(2)at^2)/(t)\\\Rightarrow u=(43.77-(1)/(2)* 9.81* 4.8^2)/(4.8)\\\Rightarrow u=-14.42525\ m/s\ upward\ or\ 14.42525\ downward`

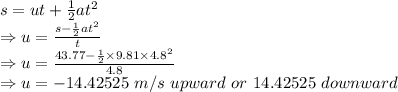
Here, the negative sign indicates that the ball would be thrown up with a velocity of 14.42525 m/s. When this ball will reach the height of the diving board it will gain the same speed as the initial upward velocity but the direction would change making it positive.

Or

The ball could be thrown directly with a velocity of 14.42525 m/s which would make the sign positive.