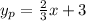Question

Write the equation of a line perpendicular to 3x+2y=8 that contains (0,3

Answer 1

`y_p=(2)/(3) x+3`

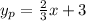
Explanation:

In the first step, re-write the equation of the given line in slope-y_intercept form in order to see clearly what its slope is. This means to solve for "y" in the equation:

`3x+2y=8\\2y=-3x+8\\y=-(3)/(2) x+(8)/(2) = -(3)/(2) x+4`

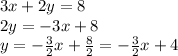
So the slope of the given line is "
`-(3)/(2)`"

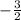Recall that the perpendicular line to a given one has a slope that equals the "opposite of the reciprocal" of the original line's slope. This means that the slope of the perpendicular line to our original line must be: "
`(2)/(3)`"

We now try to write the equation of the perpendicular line using its slope-y_intercept form, and notice that all we need to find is what is is y_intercept (b):

`y_p=(2)/(3) x+b`

To determine "b" we use the information they give us about this perpendicular line containing the point (0,3):

`y_p=(2)/(3) x+b\\3=(2)/(3) (0)+b\\3=0+b\\b=3`

Then we found that b must be 3, and we can now write the complete equation of the perpendicular line:

`y_p=(2)/(3) x+3`