Answer:
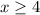
Explanation:
Let's start by using distributive property to get rid of the parenthesis on the left hand side of the inequality:
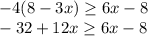
Now let's group all the terms that contain the variable x on the left, and all pure numerical terms on the right of the inequality symbol. To accomplish such, we subtract 6x from both sides, and then add 32 to both sides:

Now divide both sides of the inequality by positive 4 to isolate the "x" on one side:
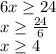
which agrees with the third option you listed.