Question

Which graphs represent functions with the following key features?

• positive on (-infinity, infinity)
• increasing on (-infinity, infinity)
• approaches 0 as x approaches -infinity

Answer 1

Graphs U and W (although this last one doesn't seem to be defined for
`x\geq 0`)

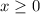Explanation:

The graphs we discard in first place: Graphs Y and Z since they represent decreasing functions (not increasing as requested in the second condition)

Graphs V and X are graphs of straight lines, therefore they don't approach zero as x goes to negative infinity (on the contrary, the two lines adopt very negative values with large absolute value as one moves towards - infinity)

Graph U and W satisfy being positive(larger than zero) in all their domains (notice though that function W seems to stop at x=0, and is not defined for positive values of x).

They also are increasing as one moves from left to right, but notice that function W seems to stop at x=0 adopting a vertical asymptote as it approaches this number.

Both functions get close to zero as one moves towards the left (x approaching more and more negative values), towards negative infinity.

Therefore, for sure function U satisfies the three conditions.

Depends on whether the general concept of behavior between -infinity and +infinity has been consider in your class, you could include function W as satisfying the conditions as well.