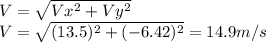Question

As an aid in working this problem, consult Interactive Solution 3.41. A soccer player kicks the ball toward a goal that is 20.0 m in front of him. The ball leaves his foot at a speed of 15.7 m/s and an angle of 31.0 ° above the ground. Find the speed of the ball when the goalie catches it in front of the net.

Answer 1

V=14.9 m/s

Step-by-step explanation:

In order to solve this problem, we are going to use the formulas of parabolic motion.

The velocity X-component of the ball is given by:

`Vx=V*cos(\alpha)\\Vx=15.7*cos(31^o)=13.5m/s`

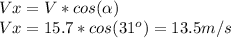
The motion on the X axis is a constant velocity motion so:

`t=(d)/(Vx)\\t=(20.0)/(13.5)=1.48s`

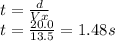
The whole trajectory of the ball takes 1.48 seconds

We know that:

`Vy=Voy+(a)*t\\Vy=15.7*sin(31^o)+(-9.8)*(1.48)=-6.42m/s`

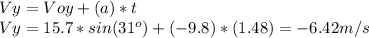
Knowing the X and Y components of the velocity, we can calculate its magnitude by:

`V=√(Vx^2+Vy^2) \\V=√((13.5)^2+(-6.42)^2)=14.9m/s`