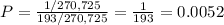Question

Four cards are dealt from a standard fifty-two-card poker deck. What is the probability that all four are aces given that at least three are aces? (Note: There are 270,725 different sets of four cards that can be dealt. Assume that the probability associated with each of those hands is 1/270,725.) Larsen, Richard J.. An Introduction to Mathematical Statistics and Its Applications (p. 38). Pearson Education. Kindle Edition.

Answer 1

The probability is 0.0052

Explanation:

Let's call A the event that the four cards are aces, B the event that at least three are aces. So, the probability P(A/B) that all four are aces given that at least three are aces is calculated as:

P(A/B) = P(A∩B)/P(B)

The probability P(B) that at least three are aces is the sum of the following probabilities:

• The four card are aces: This is one hand from the 270,725 differents sets of four cards, so the probability is 1/270,725

• There are exactly 3 aces: we need to calculated how many hands have exactly 3 aces, so we are going to calculate de number of combinations or ways in which we can select k elements from a group of n elements. This can be calculated as:

`nCk=(n!)/(k!(n-k)!)`

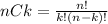
So, the number of ways to select exactly 3 aces is:

`4C3*48C1=(4!)/(3!(4-3)!)*(48!)/(1!(48-1)!)=192`

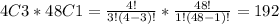
Because we are going to select 3 aces from the 4 in the poker deck and we are going to select 1 card from the 48 that aren't aces. So the probability in this case is 192/270,725

Then, the probability P(B) that at least three are aces is:

`P(B)=(1)/(270,725) +(192)/(270,725) =(193)/(270,725)`

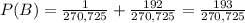
On the other hand the probability P(A∩B) that the four cards are aces and at least three are aces is equal to the probability that the four card are aces, so:

P(A∩B) = 1/270,725

Finally, the probability P(A/B) that all four are aces given that at least three are aces is:

`P=(1/270,725)/(193/270,725) =(1)/(193)=0.0052`