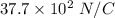Question

A thin plastic rod of length 2.8 m is rubbed all over with wool, and acquires a charge of 88 nC, distributed uniformly over its surface. Calculate the magnitude of the electric field due to the rod at a location 15 cm from the midpoint of the rod. Do the calculation two ways, first using the exact formula for a rod of any length, and second using the approximate formula for a long rod.

Answer 1

(I). The electric field when we using the exact formula is
`37.5*10^(2)\ N/C`

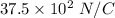
(II). The electric field when we using the approximate formula is
`37.7*10^(2)\ N/C`

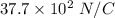
Step-by-step explanation:

Given that,

length l= 2.8 m

Charge = 88 nC

Distance from midpoint of the rod = 15 cm

(a). We need to calculate the electric field

Using the exact formula for a rod of any length

`E=(kQ)/(a)(\frac{1}{\sqrt{a^2+((L)/(2))^2}})`

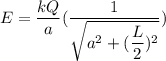
Where, Q = charge

l = length

a = distance

Put the value into the formula

`E=(9*10^(9)*88*10^(-9))/(15*10^(-2))(\frac{1}{\sqrt{(15*10^(-2))^2+((2.8)/(2))^2}})`

`E=37.5*10^(2)\ N/C`

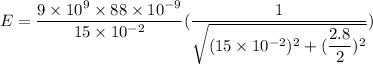
(b). We need to calculate the electric field

Using the approximate formula for a long rod

`E=(kQ)/(a)(\frac{1}{\sqrt{a^2+((L)/(2))^2}})`

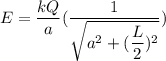
a<<L, then
`a^2+((L)/(2))^2=((L)/(2))^2`

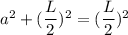
Put the value into the formula

`E=(9*10^(9)*88*10^(-9))/(15*10^(-2))(\frac{1}{\sqrt{((2.8)/(2))^2}})`

`E=37.7*10^(2)\ N/C`

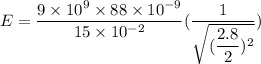
Hence, (I). The electric field when we using the exact formula is
`37.5*10^(2)\ N/C`

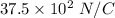
(II). The electric field when we using the approximate formula is
`37.7*10^(2)\ N/C`

Answer 2

Exact formula E=3749.9 N/C

Approximate formula E=3771.43 N/C

Step-by-step explanation:

Given that

L= 2.8 m

q= 88 nC

a= 15 cm

By using exact formula:

We know that due to charged rod given as

`E=(Kq)/(a)* \frac{1}{\sqrt{a^2+(L^2)/(4)}}`

Now by putting the values

`E=(9* 10^9* 88* 10^(-9))/(0.15)\frac{1}{\sqrt{0.15^2+(2.8^2)/(4)}}\ N/C`

E=3749.9 N/C

By approximate formula:

`a^2+(L^2)/(4)=(L^2)/(4)`

because L is so long as compare to a.

`E=(Kq)/(a)* \frac{1}{\sqrt{(L^2)/(4)}}`

`E=(9* 10^9* 88* 10^(-9))/(0.15)\frac{1}{\sqrt{(2.8^2)/(4)}}\ N/C`

E=3771.43 N/C