Answer:
Gold=$0.5
Silver=$0.35
Bronze=$0.25
Explanation:
This is the system of equations:
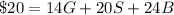 (1)
(1)
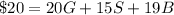 (2)
(2)
 (3)
(3)
Let's begin by substracting (2) from (1):

 (4)
(4)
Isolating
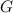 from (4):
from (4):
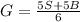 (5)
(5)
Substituting (5) in (3):
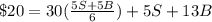
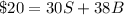 (6)
(6)
Substracting (3) from (2):

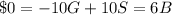
Isolating
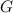 :
:
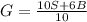 (7)
(7)
Making (5)=(7):
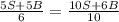
Isolating
 :
:
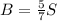 (8)
(8)
Substituting (8) in (6):
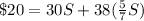
Isolating
 :
:
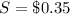 (9) This is the monetary value of silver token
(9) This is the monetary value of silver token
Substituting (9) in (6):

Finding
 :
:
 (10) This is the monetary value of bronze token
(10) This is the monetary value of bronze token
Substituting (10) and (9) in (1):
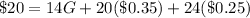
Finding
 :
:
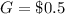 (11) This is the monetary value of golden token
(11) This is the monetary value of golden token