Question

A math club has 4 female members and 6 male members, 3 offices including a chairperson, a secretary and a treasurer must be filled. Assume that each person can fill at most one office. In how many different ways can the three offices be filled so that both female and male are included?

Answer 1

576

Explanation:

Number of female members = 4

Number of male members = 6

Number of positions = 3

Both female and male has to be included which means that either 2 females and 1 male are there or 1 male or 2 females.

So, Case - 1 - 2 females and 1 male

Possible cases =
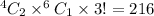`^4C_2* ^6C_1* 3!=216`, where 3! is done to permutate the members to hold various positions.

So, Case - 2 - 1 female and 2 males

Possible cases =
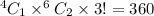`^4C_1* ^6C_2* 3!=360`, where 3! is done to permutate the members to hold various positions.

Total ways = 216 + 360 = 576