Question

Assume that different groups of couples use a particular method of gender selection and each couple gives birth to one baby. This method is designed to increase the likelihood that each baby will be a​ girl, but assume that the method has no​ effect, so the probability of a girl is 0.5. Assume that the groups consist of 38 couples. Complete parts​ (a) through​ (c) below. a. Find the mean and the standard deviation for the numbers of girls in groups of 38 births.

Answer 1

a) Mean = 19

b) Standard Deviation = 3.08

Explanation:

This is binomial probability distribution. We need to find the mean and standard deviation.

a) Mean

The formula for mean is:

`Mean = np`

Where n is the number of people, which is 38 and p is the probability of girl, which is 0.5

n = 38

p = 0.5

So,

`Mean = np\\Mean = (38)(0.5)\\Mean = 19`

Mean = 19

b) Standard Deviation

Standard deviation has the formula:

`Standard \ Deviation= √(np(1-p))`

Where n and p are the same variables in part (a)

So we plug them in and find:

`Standard \ Deviation= √(np(1-p)) \\Standard \ Deviation= √((38)(0.5)(1-0.5)) \\Standard \ Deviation= √(38*0.5*0.5)\\ Standard \ Deviation= √(9.5)\\Standard \ Deviation= 3.08`

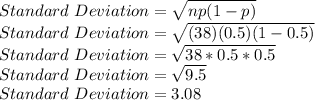
Standard Deviation = 3.08