Answer: 8.8 m
Step-by-step explanation:
The movement of the baseball to the wall is a example of parabolic motion. While the baseball aproach the wall it is affected by gravity.
In this case, because the Initial Velocity of the ball is a vecotr, it can be defined using its two directionals compounds. One, on the Y-axis and another on the X-axis. This can be related, on how a hypotenuse is the product of two legs of the triangle. Because of this, each one of this, can be know using the following equation:
Vx = Vo * cos(∅)
Vy = Vo * sin(∅)
Where Vo is the initial velocity 27.5 m/s, and ∅ is the angle which is 20.5°. So we calculate:
Vx = 27.5m/s * cos(20.5)
Vx = 27.5m/s * 0.936
Vx = 25.74m/s
Vy = 27.5m/s * sin(20.5)
Vy = 27.5m/s * sin(20.5)
Vy = 9.62m/s
Now the movement is divided on two parts, one under the effect of gravity and another one with a constant velocity.
To know how tall does the baseball hit the wall, we need to know first how much time it takes the ball to reach the wall on the X-axis. The wall is 17.5m away, we velocity on Vx that is constant we can calculate as it follow:
Time (T) = Distance (D) / Velocity (V)
Where Distance is 17.5m and our Velocity is the Vx calculated before.
T = 17.5 m / 25.74m/s
T = 0.68s
This is the time it takes the ball to reach the wall.
Know with the time, we can calculate the how tall it got on that time with the following equation:
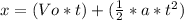
Where Vo is the Y-Compound of the Initial Velocity.
a is the aceleration, in this case the Gravity. Which, will be negative because is oposing the movement. Gravity is equal to 9.81
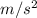
And t is the time it takes the ball to get to the wall.
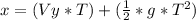
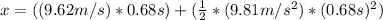
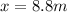
This is the height that the baseball touch the wall.