Question

A metallurgist has one alloy containing 26%26% copper and another containing 69%69% copper. How many pounds of each alloy must he use to make 5353 pounds of a third alloy containing 50%50% copper? (Round to two decimal places if necessary.)

Answer 1

Ans. He must use 2,987.76 pounds of alloy X (Cu=69%) and 2,365.24 pounds of alloy Y (26%=Cu)

Step-by-step explanation:

Hi, let´s call alloy X the alloy that contains 69% of Cu and alloy Y the one containing 26% of Cu. Since he needs to produce 5,353 pounds of alloy, the first equation that we need to use is the following.

`X+Y=5,353`

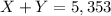
Now, we need this 5,353 pounds of the new alloy to be 50% Cu, therefore, we have to use a portion of alloy X and alloy Y. This is as follows.

`0.69X+0.26Y=0.5(X+Y)`

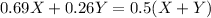
And we have already established that X+Y is equal to 5,353, therefore this equation should look like this.

`0.69X+0.26Y=5,353*0.5`

`0.69X+0.26Y=2,676.5`

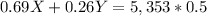
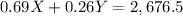
And we solve for X this equation, this as follows.

`0.69X=2,676.5-0.26Y`

`X=(2,676.5-0.26Y)/(0.69)`

`X=3,878.98-0.3768Y`

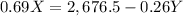
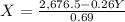
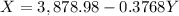
Now, we use this result and substitute this for X in the first equation like this.

`3,878.98-0.3768Y+Y=5,353`

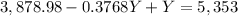
and then, we solve for Y

`0.6232Y=5,353-3,878.98`

`Y=(1,474.02)/(0.6232) =2,365.24`

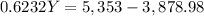
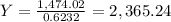
So, he needs to use 2,365.24 pounds of alloy that contains 26% of Cu, this means that the rest (2,987.76 pounds) must come from the alloy that contains 69% of Cu.

We can check this result by finding the overall Cu obtained by this amounts of alloy, that is

`Coppper FromX=2,987.76*0.69=2,061.55`

`Coppper FromY=2,365.24*0.26=614.96`

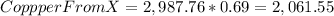
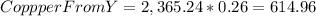
That adds up to 2,676.51 pounds of pure Cu, and since the total weight of the new alloy is 5,353, this amount of copper makes up for:

`PercentCu=(2,676.51)/(5,353) =0.5`

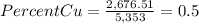
50% of the total weight.

Best of luck.