Question

Use z scores to compare the given values. The tallest living man at one time had a height of 233 cm. The shortest living man at that time had a height of 91.4 cm. Heights of men at that time had a mean of 174.45 cm and a standard deviation of 6.36 cm. Which of these two men had the height that was more​ extreme?

Answer 1

The man with the more extreme height is the man with 91.4 cm.

Step-by-step explanation:

We have two values: 233 cm and 91.4 cm. The z score for every value is calculated as:

`z=(x-m)/(s)`

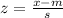
Where x is the given value, m is the mean and s is the standard deviation. So, the z score for every height is:

For 233 cm:

`z=(233-174.45)/(6.36)=9.2059`

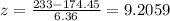
For 91.4 cm:

`z=(91.4-174.45)/(6.36)=-13.0582`

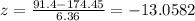
Then, the more extreme value is 91.4 cm because the z score has the highest absolute value. This is:

For 233 cm

absolute z = 9.2059

For 91.4 cm

absolute z = 13.0582

Finally, The man with the more extreme height is the man with 91.4 cm.