Question

Two oppositely charged but otherwise identical conducting plates of area 2.50 square centimeters are separated by a dielectric 1.80 millimeters thick, with a dielectric constant of K=3.60. The resultant electric field in the dielectric is 1.20×106 volts per meter. Part A Compute the magnitude of the charge per unit area σ on the conducting plate. Express your answer in coulombs per square meter to three significant figures.

Answer 1

The magnitude of the charge per unit area (σ) on the conducting plate is approximately
`3.82 * 10^-5\ C/m^2`

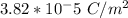
How to compute the magnitude of the charge per unit area

To compute the magnitude of the charge per unit area (σ) on the conducting plate, use the formula that relates electric field, charge density, and the dielectric constant.

Given:

Area of the conducting plates (A) = 2.50
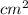`cm^2` = 2.50 ×
`10^-4\ m^2`

Separation between the plates (d) = 1.80 mm = 1.80 ×
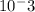`10^-3` m

Dielectric constant (K) = 3.60

Electric field in the dielectric (E) = 1.20 ×
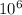`10^6` V/m

The formula relating electric field, charge density, and dielectric constant is:

E = (σ / (ε₀ * K))

Where:

ε₀ is the vacuum permittivity, which is approximately 8.85 ×
`10^-12` F/m

Rearranging the formula, we have:

σ = E * ε₀ * K

Substitute the given values:

`\sigma = (1.20 * 10^6 V/m) * (8.85 * 10^(-12) F/m) * (3.60)`

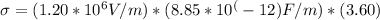
Calculating the result:

σ ≈
`3.82 * 10^-5\ C/m^2`

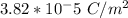
Therefore, the magnitude of the charge per unit area (σ) on the conducting plate is approximately
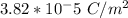`3.82 * 10^-5\ C/m^2`.

Answer 2

Answer: 38.2 μC

Explanation: In order to solve this problem we have to use the relationship for a two plate capacitor with a dielectric so:

C= Q/V= we also know that for two paralel plates C=εo*k*A/d and V=E/d

where k is the dielectric constant, A plate area, V is potential difference; E electric field and d the separation between the plates.

reorganizing we have:

Q/A=σ= E*k/εo= 1.2 * 10^6*3.6/8.85 * 10^-12=38.2μC