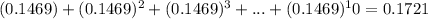Question

g A lawyer commutes daily from his suburban home to his midtown office. The average time for a one-way trip is 24 minutes, with a standard deviation of 3.8 minutes. Assume the distribution of the trip-length to be normally distributed. (a) If the office opens at 9:00am and he leaves his house at 8:40 am daily, what percentage of the time is he late for work? You must draw the distribution and indicate the relevant numbers etc. You must also give the answer as a number. (b) Find the length of time above which we find the longest 20% of the trips. You must draw the distribution and indicate the relevant numbers etc. You must also give the answer as a number. (c) During a period of 20 work days, on how many days should you expect the lawyer to be late for work? (d) What is the probability that he is late on at most 10 of those 20 days?

Answer 1

a) 85.31%

b) 56 minutes

c) 17 days

d) 0.1721

Explanation:

In order to make the calculations easier, let's standardize the curve by doing the change

`Z=(X-\mu)/(\sigma)`

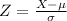
where
`\mu` is the average trip-time and
`\sigma` the standard deviation and

P(X≤ t) is the probability that the trip takes less than t minutes.

a)

Here we are looking for the value of P(X>20).

For X=20 we have Z = (20-24)/3.8 = -1.05

So, we want the area under the standard normal curve for Z > -1.05

that we can compute either using a table or a computer and we find this area equals 0.8531

So, he arrives late to work 85.31% of the times.

(See picture 1 attached)

b)

In this case we are looking for a value t of time such that

P(X≥ t) = 20% = 0.2

So, we are seeking a value Z such that the area under the normal curve to the left of Z equals 0.2

By using a table or a computer we find Z = 0.842

(See picture 2 attached)

By inserting this value in the equation on standardization

`0.842=(X-24)/(38)\Rightarrow X=38*0.842+24=55.996`

So 20% of the longest trips takes 55.996 ≅ 56 minutes

c)

Since the average of days he arrives late is 85.31%, it is expected that in 20 work days he arrives late 85.31% of 20, which equals 17 days.

d)

Since the probability that he does not arrive late is 1-0.8531 = 0.1469 and the probability of arriving early is independent of the previous trip,

the probability of arriving early n days in a row is

0.1496*0.1496*...*0.1496 n times and

the probability of being early most than 10 trips in 20 days is

`(0.1469)+(0.1469)^2+(0.1469)^3+...+(0.1469)^10=0.1721`