Question

A block is projected up a frictionless inclined plane with initial speed v0 = 1.72 m/s. The angle of incline is θ = 44.8°. (a) How far up the plane does it go? (b) How long does it take to get there? (c) What is its speed when it gets back to the bottom?

Answer 1

Step-by-step explanation:

Given

initial velocity(v_0)=1.72 m/s

`\theta =44.8{\circ}`

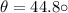
using
`v^2-u^2=2as`

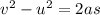
Where v=final velocity (Here v=0)

u=initial velocity(1.72 m/s)

a=acceleration
`(gsin\theta )`

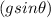
s=distance traveled

`0-(1.72)^2=2(-9.81* sin(44.8))s`

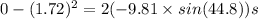
s=0.214 m

(b)time taken to travel 0.214 m

v=u+at

`0=1.72-gsin(44.8)* t`

`t=(1.72)/(9.8* sin(44.8))`

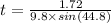
t=0.249 s

(c)Speed of the block at bottom

`v^2-u^2=2as`

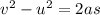
Here u=0 as it started coming downward

`v^2=2* gsin(44.8)* 0.214`

`v=√(2.985)`

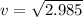
v=1.72 m/s