Question

Are your finances, buying habits, medical records, and phone calls really private? A real concern for many adults is that computers and the Internet are reducing privacy. A survey conducted by Peter D. Hart Research Associates for the Shell Poll was reported in USA Today. According to the survey, 53% of adults are concerned that employers are monitoring phone calls. Use the binomial distribution formula to calculate the probability of the following. (a) Out of four adults, none is concerned that employers are monitoring phone calls. (Round your answer to three decimal places.) (b) Out of four adults, all are concerned that employers are monitoring phone calls. (Round your answer to three decimal places.) (c) Out of four adults, exactly two are concerned that employers are monitoring phone calls. (Round your answer to three decimal places.)

Answer 1

a)There is a 4.88% probability that none is concerned that employers are monitoring phone calls.

b)There is a 7.89% probability that all are concerned that employers are monitoring phone calls.

c)There is a 37.23% probability that exactly two are concerned that employers are monitoring phone calls.

Explanation:

The binomial probability is the probability of exactly x successes on n repeated trials in an experiment which has two possible outcomes (commonly called a binomial experiment).

It is given by the following formula:

`P = C_(n,x).p^(n).(1-p)^(n-x)`

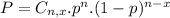
In which
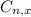`C_(n,x)` is the number of different combinatios of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

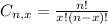
And p is the probability of a success.

In this problem, a success is being concerned that employers are monitoring phone calls.

53% of adults are concerned that employers are monitoring phone calls, so
`p = 0.53`

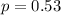
(a) Out of four adults, none is concerned that employers are monitoring phone calls.

Four adults, so
`n = 4`.

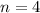Is the probability of 0 successes, so x = 0.

`P = C_(n,x).p^(n).(1-p)^(n-x)`

`P = C_(4,0).(0.53)^(0).(0.47)^(4)`

`P = 0.0488`

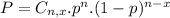
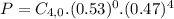
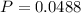
There is a 4.88% probability that none is concerned that employers are monitoring phone calls.

(b) Out of four adults, all are concerned that employers are monitoring phone calls.

Four adults, so
`n = 4`.

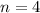Is the probability of 4 successes, so x = 4.

`P = C_(n,x).p^(n).(1-p)^(n-x)`

`P = C_(4,0).(0.53)^(4).(0.47)^(0)`

`P = 0.0789`

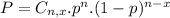
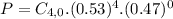
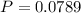
There is a 7.89% probability that all are concerned that employers are monitoring phone calls.

(c) Out of four adults, exactly two are concerned that employers are monitoring phone calls.

Four adults, so
`n = 4`.

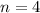Is the probability of 4 successes, so x = 2.

`P = C_(n,x).p^(n).(1-p)^(n-x)`

`P = C_(4,2).(0.53)^(2).(0.47)^(2)`

`P = 0.3723`

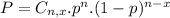
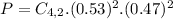
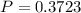
There is a 37.23% probability that exactly two are concerned that employers are monitoring phone calls.