Question

A recent college graduate is planning to take the first three actuarial examinations in the coming summer. She will take the first actuarial exam in June. If she passes that exam, then she will take the second exam in July, and if she also passes that one, then she will take the third exam in September. If she fails an exam, then she is not allowed to take any others. The probability that she passes the first exam is .9. If she passes the first exam, then the conditional probability that she passes the second one is .8, and if she passes both the first and the second exams, then the conditional probability that she passes the third exam is .7.What is the probability that she passes all three exams?Given that she did not pass all three exams, what is the conditional probability that she failed the second exam?

Answer 1

a) 0.504

b) 0.2

Explanation:

Let's call the events A, B, and C where

A = She passed the first exam

B = She passed the second exam

C = She passed the third exam

Then

A∩B = She passed both the 1st and 2nd exam

A∩ B∩ C = She passed all the 3 exams

a)

We want to determine P(A∩ B∩ C)

We have

P(A) = 0.9

P(B|A) = 0.8

and

`0.8=P(B|A)=(P(B\cap A))/(P(A))=(P(A\cap B))/(P(A))=(P(A\cap B))/(0.9)\\\ \Rightarrow P(A\cap B)=0.9*0.8=0.72`

So,

P(A∩ B)=0.72

Now we know

P(C| A∩ B)=0.7

Then

`0.7=P(C|A\cap B)=(P(C\cap A \cap B))/(P(A \cap B))=(P(A\cap B \cap C))/(P(A\cap B))=(P(A\cap B\cap C))/(0.72)\\\ \Rightarrow P(A\cap B \cap C)=0.72*0.7=0.504`

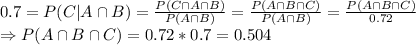
and

P(A∩ B∩ C) = 0.504

b)

Since the probability that she passes the second test given that she passed the 1st one is 0.8, then the probability that she does not pass the second test given that she passed the 1st would be 1- 0.8 = 0.2