Step-by-step explanation:
Energy stored in a capacitor is given by:
![U=(Q^2)/(2C)(1]](https://img.qammunity.org/2020/formulas/physics/high-school/67rtztp7dqetfo6ef6uwga00xw6898etdi.png)
Here, Q is the capacitor's charge and C the capacitance.
Capacitance is given by:
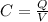
Where V is the potential difference. Rewriting for Q and replacing in 1:
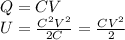
a.)
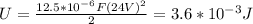
b.) Energy stored in the capacitor with dielectric is:
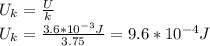
c.) Energy decreased in a rate of 3.75 due to the insertion of dielectric, that is the value of dielectric constant.
d.) If we introduce a dielectric, potential difference decreases, capacitance increases and charge is the same. Therefore, accord to (1) the energy decreases.