Question

Suppose we have an unfair coin that its head is twice as likely to occur as its tail. a)If the coin is flipped 3 times, what is the probability of getting exactly 1 head? Give your answer to four decimal places b)If the coin is flipped 5 times, what is the probability of getting exactly 2 tails? Give your answer to four decimal places c)If the coin is flipped 4 times, what is the probability of getting at least 3 tails? Give your answer to four decimal places

Answer 1

Answer: a) 0.2222, b) 0.3292, c) 0.1111

Explanation:

Since we have given that

Let the probability of getting head be p.

Since, its head is twice as likely to occur as its tail.

`p+(p)/(2)=1\\\\(3p)/(2)=1\\\\p=(2)/(3)`

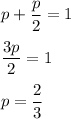
a)If the coin is flipped 3 times, what is the probability of getting exactly 1 head?

So, here, n = 3

`p=(2)/(3)`

`q=(1)/(3)`

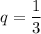
Now,

`P(X=1)=^3C_1((2)/(3))^1((1)/(3))^2=0.2222`

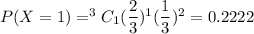
b)If the coin is flipped 5 times, what is the probability of getting exactly 2 tails?

2 tails means 3 heads.

So, it becomes,

`P(X=3)=^5C_3((2)/(3))^3((1)/(3))^2=0.3292`

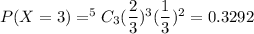
c)If the coin is flipped 4 times, what is the probability of getting at least 3 tails?

`P(X\leq 1)=\sum _(x=0)^1^4C_x((2)/(3)^x((1)/(3))^(4-x)=0.1111`

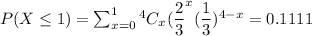
Hence, a) 0.2222, b) 0.3292, c) 0.1111