What you need to do is write the equation of the circle in standard form,

so that it's easy to identify the two central traits of the circle, its center
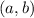 and its radius
and its radius
 .
.
By completing the square, we have



and from this we can tell the circle is centered at
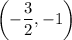 with radius 2.
with radius 2.
The line
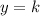 is horizontal and will intersect the circle whenever
is horizontal and will intersect the circle whenever
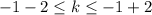 , or
, or
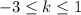 . So the line will not intersect the circle if
. So the line will not intersect the circle if
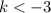 or
or
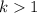 .
.