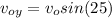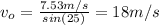Question

A fisherman casts his bait toward the river at an angle of 25° above the horizontal. As the line unravels, he notices that the bait and hook reach a maximum height of 2.9 m. What was the initial velocity he launched the bait with? Assume that the line exerts no appreciable drag force on the bait and hook and that air resistance is negligible. A fisherman casts his bait toward the river at an angle of 25° above the horizontal. As the line unravels, he notices that the bait and hook reach a maximum height of 2.9 m. What was the initial velocity he launched the bait with? Assume that the line exerts no appreciable drag force on the bait and hook and that air resistance is negligible. 6.3 m/s 18 m/s 7.9 m/s 7.6 m/s

Answer 1

`v_(o)=18m/s`

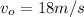
Step-by-step explanation:

According to the exercise we know the angle which the bait was released and its maximum height

`\beta =25\\y=2.9m`

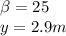
To find the initial y-component of velocity we need to do the following steps:

`v_(y)^(2) =v_(oy)^(2)+2g(y-y_(o))`

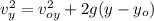
At maximum height the y-component of velocity is 0 and from the exercise we know that the initial y position is 0

`0=v_(oy)^(2)-2(9.8m/s^2)(2.9m)`

`v_(oy)=\sqrt{2(9.8m/s^(2) )(2.9m)} =7.53m/s`

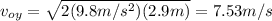
Since the bait is released at 25º

`v_(oy)=v_(o)sin(25)`

`v_(o)=(7.53m/s)/(sin(25))=18m/s`