Question

Every year, Proxima Centauri, the closest star to the sun, is observed to move 1.5 arcseconds with respect to the background stars for six months, followed by a return to its original position over the course of the next six months. How far away is Proxima Centauri? [diameter of Earth's orbit = 2 AU (astronomical units)]?

Answer 1

How far away is Proxima Centauri?

Proxima Centauri is at a distance of
`2.0394x10^(13) Km`.

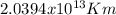[diameter of Earth's orbit = 2 AU (astronomical units)]?

`r = 1AU`

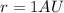
Remembering than the diameter is defined as:

`d = 2r`

Where r is the radius.

So it is correct to say that the diameter of Earth's orbit = 2 AU (astronomical units).

Step-by-step explanation:

How far away is Proxima Centauri?

The angle due to the change in position of a nearby object against the background stars it is known as parallax.

Hence, Proxima Centauri have a parallax of 1.5 arc seconds. This angle is gotten when its position is measured in January and then in July according with the configuration of the Earth with respect to the Sun in those months.

The parallax angle can be use to find out the distance to Proxima Centauri by means of triangulation. Making a triangle between Proxima Centauri, the Sun and the Earth (as is show in the image below), knowing that the distance between the earth and the Sun (150000000 Km) is define as 1 astronomical unit:

`tan(p) = (1AU)/(d)`

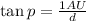
Where d is the distance to the star.

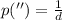`p('') = (1)/(d)` (1)

Equation (1) can be rewritten in terms of d:

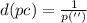`d(pc) = (1)/(p(''))` (2)

Equation (2) represents the distance in a unit known as parsec (pc), that is the distance of a star with a parallax angle of 1 arc second.

`d(pc) = (1)/(1.5)`

`d(pc) = (1)/(1.5)`

`d(pc) = 0.66 pc`

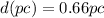
But
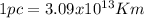`1pc = 3.09x10^(13) Km`, therefore:

`0.66pc . (3.09x10^(13) Km)/(1pc)` ⇒
`2.0394x10^(13) Km`

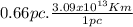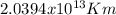
Or it can be expressed in light years, since
`1pc = 3.26 light years`:

`0.66pc . (3.26 light years)/(1pc)` ⇒
`2.1516 light years`

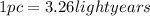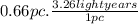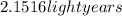
In which 1 light year corresponds to the distance traveled for light in one year.

So Proxima Centauri is at a distance of
`2.0394x10^(13) Km`.

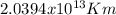[diameter of Earth's orbit = 2 AU (astronomical units)]?

As it was mentioned above, 1 astronomical unit is define as the distance between the Earth and the Sun. That distance will correspond with the radius of the orbit of Earth around the Sun.

`r = 1AU`

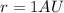
Remembering than the diameter is defined as:

`d = 2r`

Where r is the radius.

So it is correct to say that the diameter of Earth's orbit = 2 AU (astronomical units).