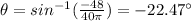Answer:
The angle at which the boat must head is

Solution:
As per the solution:
Distance between the parallel banks, d = 40 m
The maximum speed of water, v' = 3 m/s
constant speed, u' = 5 m/s
Also,
The speed of water of the river at a distance of 'x' units from the west bank is given as a sine function:
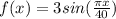 (2)
(2)
Now, to determine the angel at which the boat must head:
The velocity of the engine of the boat:
v =
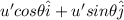
v =
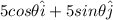
The abscissa of the boat at time t:
v =

Now, from above and eqn(1) , we can write:
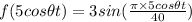
Now, boat's velocity at time t:
v =
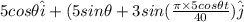
In order to obtain the position of the boat, we integrate both the sides, we get:
r =
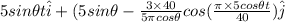 + C (3)
+ C (3)
Now, at r = 0:
0 =
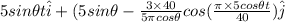 + C
+ C
C =
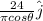
Now, from eqn (3)
r =
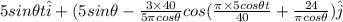 (4)
(4)
the baot will reach the point at y = 0 and x = 40
Now,
40 =
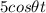
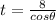
Substituting the above value of 't' in eqn (4):
r =
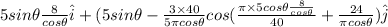
We get: