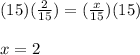Question

What is the value of x in the proportion below?
2/3/5= x/15

Answer 1

Answer:
`x=2`

Explanation:

Given the following proportion:

`((2)/(3))/(5)=(x)/(15)`

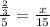
You can follow these steps in order to find the value of "x":

1. You need to remember that:

`((a)/(b))/(c)=((a)/(b))/((c)/(1))= (a*1)/(b*c)=(a)/(b*c)`

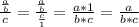
Then:

`((2)/(3))/(5)=(x)/(15)\\\\\frac{{(2)/(3)}}{{(5)/(1)}}=(x)/(15)\\\\(2*1)/(3*5)= (x)/(15)\\\\(2)/(15)= (x)/(15)`

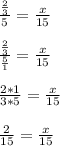
2. Finally, you need to multiply both sides of the equation by 15. Then you get that the value of "x" is:

`(15)((2)/(15))= ((x)/(15))(15)\\\\x=2`