Question

Michelle invested $12,000 in stocks and bonds, paying 4.8% and 7% annual interest,

respectively. If the total interest earned for the year was $763, how much was invested in stocks
and how much was invested in bonds?

Answer 1

Michelle invested $3500 in stocks and $8500 in bonds.

Explanation:

To solve this problem, we have to determine a system of equations, because there's two different nature that cannot be solved using only one equation.

Givens:

• Investment $12000 in stocks and bonds.
• Stocks pay 4.8% and bonds pay 7% as annual interest.
• The total interest earnings was $763.

So, let's say that
`x` is stocks, and
`y` is bonds.

The first equation would be:

`x+y=12000`

Because between stocks and bonds, Michelle invested $12000.

The second equation would be:

`0.048x+0.07y=763`

Which means that with an annual interest of 4.8% for stocks and 7% for bonds, Michelle earned $763.

Now, we isolate
`x` in the first equation and replace it in the second equation:

`x=12000-y\\0.048(12000-y)+0.07y=763\\576-0.048y+0.07y=763\\0.022y=187\\y=(187)/(0.022)=8500`

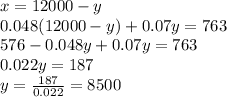
Now, we replace this value in the first equation:

`x+8500=12000\\x=12000-8500=3500`

Therefore, Michelle invested $3500 in stocks and $8500 in bonds.

Answer 2

Michelle invested $8,500 in bonds and $3,500 in stocks.

Explanation:

Ok, let "x" be the investment in stock, and "y" the investment in bonds.

We will have two equations:

x + y = $12,000

0.048x + 0.07y = $763

Clear x on the 1st equation: x = $12,000 - y

0.048*($12,000-y) + 0.07y = $763

$576 - 0.048y + 0.07y = $763

-0.048y + 0.07y = $763 - $576

0.022y = $187

y = $187/0.022 = $8500

Now, let's clear x:

x = $12000 - y = $12000 - $8500 = $3500