Answer:
For a: The heat required for the given process is 623.74 kJ
For b: The time required for each process is calculated below.
Step-by-step explanation:
The processes involved in the given problem are:

Pressure is taken as constant.
To calculate the amount of heat absorbed at different temperature, we use the equation:
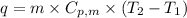 .......(1)
.......(1)
where,
q = amount of heat absorbed = ?
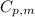 = specific heat capacity of medium
= specific heat capacity of medium
m = mass of water/ice
 = final temperature
= final temperature
 = initial temperature
= initial temperature
To calculate the amount of heat released at same temperature, we use the equation:
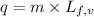 ......(2)
......(2)
where,
q = amount of heat absorbed = ?
m = mass of water/ice
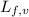 = latent heat of fusion or vaporization
= latent heat of fusion or vaporization
Calculating the heat absorbed for each process:
Conversion factor used: 1 kg = 1000 g
1 kJ = 1000 J
We are given:
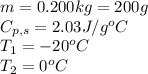
Putting values in equation 1, we get:
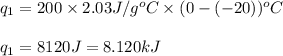
We are given:
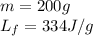
Putting values in equation 2, we get:
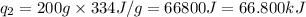
We are given:
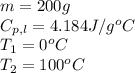
Putting values in equation 1, we get:
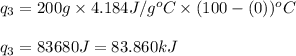
We are given:

Putting values in equation 2, we get:
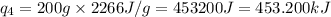
We are given:
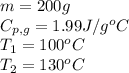
Putting values in equation 1, we get:

Total heat absorbed =
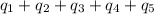
Total heat absorbed =
![[8.120+66.800+83.680+453.200+11.940]kJ=623.74kJ](https://img.qammunity.org/2020/formulas/physics/college/blgwbrvnaunry70aplorhtirqyfap6uar5.png)
Hence, the heat required for the given process is 623.74 kJ
We are given:
Rate of heat transfer = 20.0 kJ/s
To calculate the time required for each stage, we apply unitary method:
Heat transferred = 8.120 kJ
When 20 kJ of heat is transferred in 1 sec
So, 8.120 kJ of heat will be transferred in =
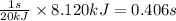
Time required for heat transfer of process 1 is 0.406 seconds
Heat transferred = 66.800 kJ
When 20 kJ of heat is transferred in 1 sec
So, 66.800 kJ of heat will be transferred in =
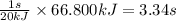
Time required for heat transfer of process 2 is 3.34 seconds
Heat transferred = 83.680 kJ
When 20 kJ of heat is transferred in 1 sec
So, 83.680 kJ of heat will be transferred in =
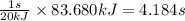
Time required for heat transfer of process 3 is 4.184 seconds
Heat transferred = 453.200 kJ
When 20 kJ of heat is transferred in 1 sec
So, 453.200 kJ of heat will be transferred in =
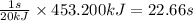
Time required for heat transfer of process 4 is 22.66 seconds
Heat transferred = 11.940 kJ
When 20 kJ of heat is transferred in 1 sec
So, 11.940 kJ of heat will be transferred in =

Time required for heat transfer of process 5 is 0.597 seconds