For this case we must find the justification of:
![10 ^ {\frac {1} {3}} = \sqrt [3] {10}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/kjv8ij7is6161o0zioxqbjm1sm8koga52q.png)
By definition of properties of powers and roots we have to meet:
![a ^ {\frac {m} {n}} = \sqrt [n] {a ^ m}](https://img.qammunity.org/2020/formulas/mathematics/college/ekk1eatq6ejvf0yyrecds2dw2lflpgu8qi.png)
So, if we have:
![\sqrt [3] {10} = \ \sqrt [3] {10 ^ 1} = 10 ^ {\frac {1} {3}}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/peri2c4f9iftixs1xzwvviay2tw6vbdgy7.png)
Other property states that:
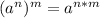
So, the expression: "Ten to the one third power all raised to the third power" is represented as:
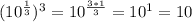
ANswer;
Option B