Question

The weight of an organ in adult males has a​ bell-shaped distribution with a mean of 325 grams and a standard deviation of 25 grams. Use the empirical rule to determine the following. ​(a) About 68​% of organs will be between what​ weights? ​(b) What percentage of organs weighs between 275 grams and 375 ​grams? ​(c) What percentage of organs weighs less than 275 grams or more than 375 ​grams? ​(d) What percentage of organs weighs between 300 grams and 400 ​grams?

Answer 1

(a) between 300 grams and 350 grams (b) 95% (c) 5% (d) 83.85%

Explanation:

We have that
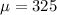`\mu = 325` grams and
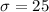`\sigma = 25` grams. Let's compute the following figures to use the empirical rule

`\mu + \sigma  = 325 + 25    = 350`

`\mu + 2\sigma = 325 + 2(25) = 375`

`\mu + 3\sigma = 325 + 3(25) = 400`

`\mu - \sigma  = 325 - 25    = 300`

`\mu - 2\sigma = 325 - 2(25) = 275`

`\mu - 3\sigma = 325 - 3(25) = 250`

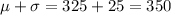
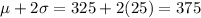
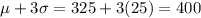
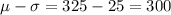
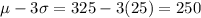
using the image below that was made it with help of the empirical rule we find the next figures

(a) About 68% of organs will be between 300 grams and 350 grams

(b) 95% of organs weights between 275 grams and 375 grams

(c) 5% of organs weights less than 275 grams or more than 375 grams

(d) 83.85% of organs weights between 300 grams and 400 grams