Question

find an equation in slope-intercept form of the line that has slope 2 and passes through point A ( -3, -1)

Answer 1

The equation in slope intercept form having slope of 2 and passes through the point A(-3,-1) is given as 2x - y + 5 = 0.

Solution:

In geometry we know the standard form of slope intercept form is y = mx + c. where “m” stands for the slope of the equation, “c” stands for the intercept.

Let us consider the point
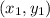`\left(x_(1), y_(1)\right)`. A straight line passing through that point having the slope of m is given as

`\bold{y - y_(1) = m\left(x - x_(1)\right)}`

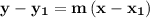
In the given question, the point A(-3,-1) has the slope of 2.

Hence we get m = 2 and
`x_(1) = -3 ; y_(1) = -1`

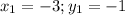
The equation for the line in slope-intercept form is given as

y - (-1) = 2(x - (-3))

y + 1 = 2(x + 3)

y + 1 = 2x + 6

Rearranging the terms, we get

2x – y + 6 -1 = 0

2x – y + 5 = 0

Hence the equation in slope-intercept form of the line that has slope 2 and passes through point A(-3, -1) is 2x – y + 5= 0.