Question

A catapult launches a test rocket vertically upward from a well, giving the rocket an initial speed of 80.6 m/s at ground level. The engines then fire, and the rocket accelerates upward at 4.20 m/s2 until it reaches an altitude of 1180 m. At that point its engines fail, and the rocket goes into free fall, with an acceleration of −9.80 m/s2. (You will need to consider the motion while the engine is operating and the free-fall motion separately.) (a) For what time interval is the rocket in motion above the ground?

Answer 1

44.64 seconds

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration due to gravity = 9.8 m/s²

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* 4.2* 1180+80.6^2)\\\Rightarrow v=128.01\ m/s`

`v=u+at\\\Rightarrow 128.01=80.6+4.2t\\\Rightarrow t=(128.01-80.6)/(4.2)=11.29\ s`

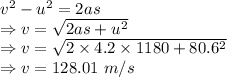
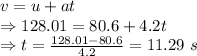
Time taken to reach 1180 m is 11.29 seconds

`v=u+at\\\Rightarrow 0=128.01-9.8t\\\Rightarrow t=(128.01)/(9.8)=13.06\ s`

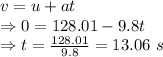
Time the rocket will keep going up after the engines shut off is 13.06 seconds.

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(0^2-128.01^2)/(2* -9.8)\\\Rightarrow s=836.05\ m`

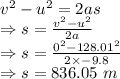
The distance the rocket will keep going up after the engines shut off is 836.05 m

Total distance traveled by the rocket in the upward direction is 1180+836.05 = 2016.05 m

The rocket will fall from this height

`s=ut+(1)/(2)at^2\\\Rightarrow 2016.05=0t+(1)/(2)* 9.8* t^2\\\Rightarrow t=\sqrt{(2016.05* 2)/(9.8)}\\\Rightarrow t=20.29\ s`

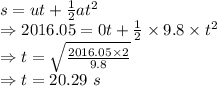
Time taken by the rocket to fall from maximum height is 20.29 seconds

Time the rocket will stay in the air is 11.29+13.06+20.29 = 44.64 seconds