Answer:
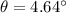
Step-by-step explanation:
It is given that,
The frequency of monochromatic light,
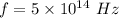
Slit separation,
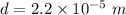
Let
 is the angle away from the central bright spot the third bright fringe past the central bright spot occur. The condition for bright fringe is :
is the angle away from the central bright spot the third bright fringe past the central bright spot occur. The condition for bright fringe is :
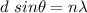
n = 3
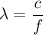
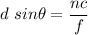
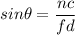
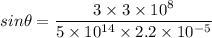
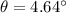
So, at 4.64 degrees the third bright fringe past the central bright spot occur. Hence, this is the required solution.