Question

A lawyer commutes daily from his suburban home to his midtown office. The average time for a one-way trip is 24 minutes, with a standard deviation of 3.8 minutes. Assume the distribution of the trip-length to be normally distributed. During a period of 20 work days, on how many days should you expect the lawyer to be late for work?

Answer 1

lawyer will be late for at least 17 days

Step-by-step explanation:

given,

average time for a one way trip = 24 minutes

standard deviation = 3.8 minute

`Z = (x-\mu)/(\sigma)`

P(of late) = P(x>20 min)

=
`P(Z>(20-24)/(3.8)) = P(z>-1.05)`

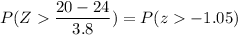
= 0.5 + 0.3531

= 0.8531 = 85.31 %

days lawyer would be late for work

= n p = 20 × 0.8531 = 17.062 days

hence, lawyer will be late for at least 17 days during a period of 20 work day.