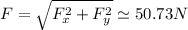Question

A tennis player is hitting a 58 gram tennis ball back across the net. When the racquet and the ball first make contact, the ball is moving at 30 m/s 15⁰ below the positive x-axis. When the ball leaves the racquet, it is moving at 40 m/s 15⁰ above the negative x-axis. If the ball is in contact with the racquet for 0.08 s, what is the average net force acting on the tennis ball while it is in contact with the racquet? Air resistance and the force of gravity are negligible when compared to the force by the tennis racquet.

Answer 1

The net force acting on the tennis ball while it is in contact with the racquet is 50.73 N

Step-by-step explanation:

The impulse-momentum theorem said that the net impulse is equal to the change of the momentum, this is:

`\overrightarrow{I}=\varDelta\overrightarrow{P}\,\,(1)`

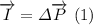
but the net impulse is too the net force times the change in time:

`\overrightarrow{I}=\overrightarrow{F}\varDelta t\,\,(2)`

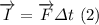
so using (2) on (1) we have:

`\overrightarrow{F}\varDelta t=\varDelta\overrightarrow{P}\,\,(3)`

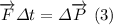
Decomposing that on x and y components:

`F_(x)\varDelta t=\varDelta P_(x)=P_(fx)-P_(ox)\,\,(3)`

`F_(y)\varDelta t=\varDelta P_(y)=P_(fy)-P_(oy)\,\,(4)`

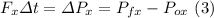
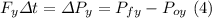
(See figure below) with Pfx = m*vfx= m*vf*cos(15°)=(0.058kg)(40m/s)cos(15°),

Pox = -m*vox= m*vo*cos(15°)=-(0.058kg)(30m/s)cos(15°), the same analysis to Pfy and Poy gives

Pfy=(0.058kg)(40m/s)sin(15°), Poy=-(0.058kg)(30m/s)sin(15°), using those values on (3) and (4) and solving for Fy and Fx:

`F_(x)=\frac{(0.058)(40)cos(15\text{\textdegree})-(-(0.058)(30)cos(15\text{\textdegree}))}{0.08}\simeq49N\,\,(5)`

`F_(y)=\frac{(0.058)(40)sin(15\text{\textdegree})-(-(0.058)(30)sin(15\text{\textdegree}))}{0.08}\simeq13.13N\,\,(6)`

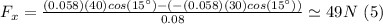
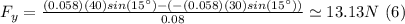
So the net force acting on the tennis ball while it is in contact with the racquet is:

`F=\sqrt{F_(x)^(2)+F_(y)^(2)}\simeq50.73N`