Question

A model rocket is launched straight upward with an initial speed of 52.0 m/s. It accelerates with a constant upward acceleration of 1.00 m/s2 until its engines stop at an altitude of 160 m.

(a) What can you say about the motion of the rocket after its engines stop? This answer has not been graded yet.
(b) What is the maximum height reached by the rocket? m
(c) How long after liftoff does the rocket reach its maximum height? s
(d) How long is the rocket in the air? s

Answer 1

Step-by-step explanation:

(a) After the engines stop, the rocket reaches a maximum height at which it will stop and begin to descend in free fall due to gravity.

(b) We must separate the motion into two parts, when the rocket's engines is on and when the rocket's engines is off.

First we must find the rocket speed when the engines stop:

`v_f^2=v_0^2+2ay_1\\v_f^2=(52(m)/(s))^2+2(1(m)/(s^2))(160m)\\v_f^2=3024(m^2)/(s^2)\\v_f=\sqrt{3024(m^2)/(s^2)}=54.99(m)/(s)`

This final speed is the initial speed in the second part of the motion, when engines stop until reach its maximun height. Therefore, in this part the final speed its zero and the value of g its negative, since decelerates the rocket:

`v_f^2=v_0^2+2gy_(2)\\y_(2)=(v_f^2-v_0^2)/(2g)\\y_(2)=(0^2-(54.99(m)/(s))^2)/(2(-9.8(m)/(s^2)))=154.28m`

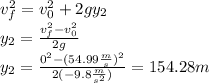
So, the maximum height reached by the rocket is:

`h=y_1+y_2\\h=160m+154.28m=314.28m`

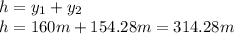
(c) In the first part we have:

`v_f=v_0+at_1\\t_1=(v_f-v_0)/(a)\\t_1=(54.99(m)/(s)-52(m)/(s))/(1(m)/(s^2))\\t_1=2.99s`

And in the second part:

`t_2=(v_f-v_0)/(g)\\t_2=(0-54.99(m)/(s))/(-9.8(m)/(s^2))\\t_2=5.61s`

So, the time it takes to reach the maximum height is:

`t_3=t_1+t_2\\t_3=2.99s+5.61s=8.60s`

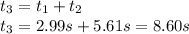
(d) We already know the time between the liftoff and the maximum height, we must find the rocket's time between the maximum height and the ground, therefore, is a free fall motion:

`v_f^2=v_0^2+2ay\\v_f^2=0^2+2(9.8(m)/(s^2))(314.28m)\\v_f=\sqrt{6159.888(m^2)/(s^2)}=78.48(m)/(s)`

`t_4=(v_f-v_0)/(g)\\t_4=(78.48(m)/(s)-0)/(9.8(m)/(s^2))\\t_4=8.01s`

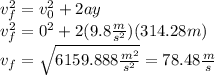
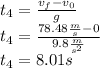
So, the total time is:

`t=t_3+t_4\\t=8.60s+8.01s\\t=16.61s`