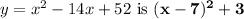Question

Write y = x2 −14x + 52 in vertex form.

A) y = (x + 7)2 + 3


B) y = (x − 7)2 − 3


C) y = (x − 7)2 + 3


D) y = (x + 7)2 − 3

Answer 1

Option c

Answer:

The vertex form for
`y = x^(2) - 14 x + 52 \text { is }\bold{(x - 7)^(2) + 3}`

Solution:

The standard form of equations is given as
`\bold{y = a x^(2) + bx + c}`

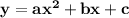
The general representation of vertex form is
`\bold{y = a(x-h)^(2) + k}` where (h,k) is the vertex of the parabola.

The "a" in the vertex form is the same "a" as in
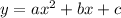`y = a x^(2) + bx + c` (standard form)

The value of “a” is same in both standard and vertex form.

In order to represent the given expression into vertex form follow the below steps:

From question, Given equation is
`y = x^(2) - 14x + 52`.This equation can be rewritten as

`y = x^(2) - 14x + 49 + 3`

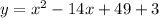
Where “52” has been rewritten as 49 + 3.

Now, 14x can be written as 2(7x) and 49 can be written as
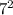`7^(2)`. Hence the above equation becomes,

`y = x^(2) - 2(7 x) + 7^(2) + 3`

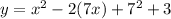
The first three terms of above equation is of the form
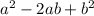`a^(2) - 2ab + b^(2)`, where a = 1 and b = 7

We know that
`a^(2) - 2ab + b^(2) = (a - b)^(2)`

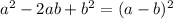
Hence
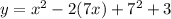`y = x^(2) - 2(7x) + 7^(2) + 3` becomes,

`x^(2) - 2(7 x) + 7^(2) + 3 = (x - 7)^(2) + 3`

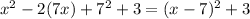
Now
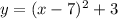`y = (x - 7)^(2) + 3` is of the form
`y = a(x - h)^(2) + k`

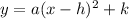
Where by comparing we get, a = 1 and h = 7 and k = 3

`y = (x - 7)^(2) + 3`

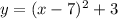
Hence the vertex form of
`y = x^(2) - 14x + 52 \text { is }\bold{(x - 7)^(2) + 3}`