Answer:
(a) 0.5899
(b) 0.9166
Explanation:
Let X be the random variable that represents the height of a woman. Then, X is normally distributed with
 = 62.5 in
= 62.5 in
 = 2.2 in
= 2.2 in
the normal probability density function is given by
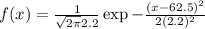 , then
, then
(a)
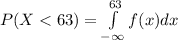 = 0.5899
= 0.5899
(in the R statistical programming language) pnorm(63, mean = 62.5, sd = 2.2)
(b) We are seeking
 where n = 37.
where n = 37.
 is normally distributed with mean 62.5 in and standard deviation
is normally distributed with mean 62.5 in and standard deviation
 . So, the probability density function is given by
. So, the probability density function is given by
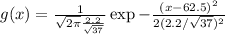 , and
, and
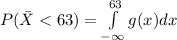 = 0.9166
= 0.9166
(in the R statistical programming language) pnorm(63, mean = 62.5, sd = 2.2/sqrt(37))
You can use a table from a book to find the probabilities or a programming language like the R statistical programming language.