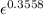Answer:
K = 57904.32 lb/in²
σt = 57904.32×
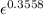
Step-by-step explanation:
given data
gage length l1 = 2 in
area A1 = 0.50 in²
gage length l2 = 2.3 in
engineering stress σ1 = 25000 lb/in²
gage length l3 = 3 in
engineering stress σ2 = 28,000 lb/in²
to find out
strength coefficient and the strain-hardening exponent for this metal
solution
we know that volume v of work is constant so
v1 = v2 = v3
so we can say A1×l1 = A2×l2 = A3×l3 ............1
here v is volume , A is area and l is length
so
we find first area of cross section (A) at both state 1 and 2
use equation 1
A1×l1 = A2×l2 = A3×l3
A2 =
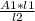 =
=
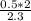
A2 = 0.43478 in²
and
A3 =
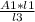 =
=
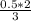
A3 = 0.3333 in²
and
engineering stress is express as
engineering stress =
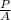
here P is true load and A is area of cross section so
and P = engineering stress × A
so
true stress will be at both state 1 and 2
σt =
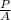 ...................2
...................2
σt 2 =
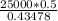
σt 2 = 28750.17 lb/in²
and
σt 3 =
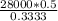
σt 3 = 42000.42 lb/in²
and
true strain will be at both state 1 and 2
ε =
 ....................3
....................3
ε 2 =
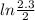
ε 2 = 0.139762
ε 3 =
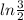
ε 3 = 0.405465
and
we know relation between true stress and stain is
σt = K ×
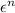 ........................4
........................4
put here value for both state
28750.17 = K ×
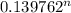 ...........................5
...........................5
42000.42 = K ×
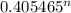 ............................6
............................6
now from equation 5 divide by 6

take ln both side
ln ( 0.68452) = n ln

n = 0.3558
so
K from equation 5 is
28750.17 = K ×
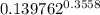
K = 57904.32 lb/in²
and
flow curve equation is from equation 4
σt = K ×
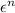
σt = 57904.32×