Question

The risk-free rate of return is 4%, the required rate of return on the market is 10%, and High-Flyer stock has a beta coefficient of 2.0. If the dividend per share expected during the coming year, D1, is $4.60 and g = 6%, at what price should a share sell? (Do not round intermediate calculations. Round your answer to 2 decimal places.)

Answer 1

the share should sell at $46

Step-by-step explanation:

We use the CAPM method to know the required return of the capital

`Ke= r_f + \beta (r_m-r_f)`

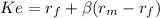
risk free 0.04

market rate 0.1

beta(non diversifiable risk) 2

`Ke= 0.04 + 2 (0.06)`

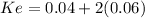
Ke 0.16000 = 16%

Now we calculate with the dividends grow model the intrinsic value of the share:

`(divends)/(return-growth) = Intrinsic \: Value`

`(4.60)/(0.16-0.06) = Intrinsic \: Value`

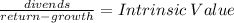
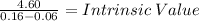
$4.6/0.1 = $46