Answer: 23000 frames/s
Step-by-step explanation:
We know the maximum initial speed at which the seeds are dispersed is:
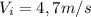
In addition, we know the maximum distance at which the seeds move between photographic frames is:
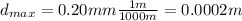
And we need to find the minimum frame rate of the camera with these given conditions. This can be found by finding the time
 for each frame and then the frame rate:
for each frame and then the frame rate:
Finding the time:
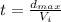
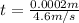
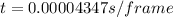 This is the time for each frame
This is the time for each frame
Now we need to find the frame rate, which is the frequency at which the photos are taken.
In this sense, frequency
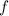 is defined as:
is defined as:
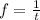
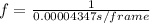
Finally:
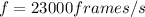
Hence, the minimum frame rate is 23000 frames per second.