Question

Three players are each dealt, in a random manner, five cards from a deck containing 52 cards. Four of the 52 cards are aces. Find the probability that at least one person receives exactly two aces in their five cards.

Answer 1

The probability that at least one person receives exactly two aces in their five cards is 0.1194.

Explanation:

We define the following events:

A: person A receives exactly two aces in their five cards.

B: person B receives exactly two aces in their five cards.

C: person C receives exactly two aces in their five cards.

We need to calculate P(A∪B∪C). According to the principle of inclusion and exclusion:

P(A∪B∪C)= P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)

Total outcomes is equal to
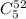`C^(52)_(5)` because there 52 cards and we select 5 of them.

The probability of each event is given by:

P(A)=P(B)=P(C)=
`(C^(4)_(2).C^(48)_(3))/(C^(52)_(5))`=
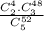`((4!)/(2!2!) .(48!)/(3!45!))/((52!)/(5!47!))`=0.0399

where the possible outcomes are 2 aces and 3 of the other cards.

Then, the intersections of the events mean that one player gets 2 aces and the other gets 2 aces too.

P(A∩B)=P(B∩C)=P(A∩C)=
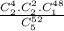`(C^(4)_(2).C^(2)_(2).C^(48)_(1))/(C^(52)_(5))`=0.0001

Finnaly,

P(A∩B∩C)=0 because it is not possible that the three events occur at the same time due to there are only 4 aces.

P(A∪B∪C)= 0.0399+0.0399+0.0399-0.0001-0.0001-0.0001+0

P(A∪B∪C)=0.1194

The probability that at least one person receives exactly two aces in their five cards is 0.1194.