Answer:
P(X = 0) = 0.0208, P(X = 1) = 0.2484, P(X = 2) = 0.7308
Explanation:
Let's define the following events
A: the first component meet specification
B: the second component meet specification
P(A) = 0.87
P(B) = 0.84
Let X be the random variable that represents the number of components in the assembly that meet specifications. Because there are only two mechanical components in the assembly, X can only take the values 0, 1, 2.
P(X = 0) = P(the first component does not meet specification and the second component does not meet specification) =
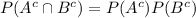 (because of independence)
(because of independence)
= (0.13)(0.16) = 0.0208
P(X = 1) = P(only one component meet specification) = P[(the first component meet specification and the second component does not meet specification) or (the first component does not meet specification and the second component meet specification)] =
![P[(A\cap B^(c))\cup (A^(c)\cap B)] = P(A\cap B^(c)) + P(A^(c)\cap B)=](https://img.qammunity.org/2020/formulas/mathematics/college/rknhr0it9q8iw5k216ueuomldpi98qx7ha.png) (because sets are mutually exclusive)
(because sets are mutually exclusive)
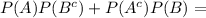 (because of independence)
(because of independence)
= (0.87)(0.16) + (0.13)(0.84) = 0.2484
P(X = 2) = P(both components meet specifications) =
 (because of independence)
(because of independence)
= (0.87)(0.84)
= 0.7308